소수 만들기
in Algorithm
문제 풀이
🔖 소스 코드
🔖 문제
| 사용된 알고리즘 |
|---|
| 에라토스테네스의 체 |
에라토스테네스의 체
에라토스테네스의 체는 소수를 찾는 방법이다.
소수 : 자기 자신과 1만을 약수로 가지는 수
메커니즘은 아래와 같다.
| 순서 | 메커니즘 |
|---|---|
| 1 | 2부터 소수를 구하고자 하는 구간의 모든 수를 나열한다. |
| 2 | 2는 소수이므로 2를 제외한 2의 배수를 모두 지운다. |
| 3 | 남아있는 수 가운데 3은 소수이므로 3을 제외한 3의 배수를 모두 지운다. |
| 4 | 남아있는 수 가운데 5는 소수이므로 5를 제외한 5의 배수를 모두 지운다. |
| 5 | 위 과정을 반복하면 구하는 구간의 모든 소수가 남는다. |
예를 들어 소수인지 판별하고 싶은 값이 (K=12)라고 할 때,
아래의 코 처럼 2부터 12까지 나눠서 나머지가 0이 아닌 경우를 소수로 판별해도 된다.
하지만 이렇게 하면 2부터 12까지 총 11번의 연산이 이루어진다.
public static boolean isPrimeNum(int num) {
for (int i =0; i < num; i++) {
if (num % i == 0) {
return false;
}
return true;
}
}
만약 아래의 코드 처럼 12의 제곱근을 나누면 어떻게 될까?
public static boolean isPrimeNum(int num) {
for (int i = 2; i <= Math.sqrt(num); i++) {
if (num % i == 0) {
return false;
}
}
return true;
}
결과는 동일하다. 하지만 시간 복잡도가 O(N)에서 O(N^(1/2))으로 줄어든다.
왜냐면 12의 제곱근은 대충 3.xxx 가 되는데, 이렇게 되면 2, 3, 3.xxx 이렇게 3번만
연산을 하면 되기 때문이다. 아래 사진으로 속도가 빨라진걸 명확하게 알아볼 수 있다.
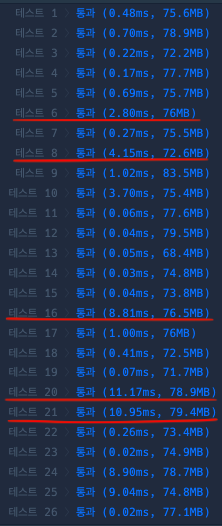
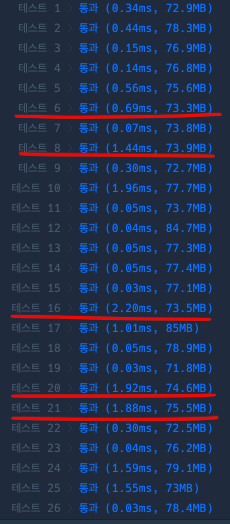
자바로 구현한 에라토스테네스의 체
public class Eratosthenes {
public static void main(String[] args) {
int N = 25;
primeNumbers(N);
}
public static void primeNumbers(int num) {
int[] arr = new int[num+1];
// 1. 2부터 구간의 모든 수 나열
for (int = 2; i <= N; i++) {
arr[i] = i;
}
// 2. 2는 소수이므로 2를 제외한 2의 배수를 지운다.
for (int i = 2; i <= N; i++) {
if (arr[i] == 0) {
continue;
}
// i의 배수를 지운다.
for (int j = i * i; j <= N; j += i;) {
arr[j] = 0;
}
}
// 3. 소수만 반환
for (int primeNum : arr) {
if (primeNum != 0) {
System.out.print(primeNum + " ");
}
}
}
}
출력 결과
2 3 5 7 11 13 17 19 23
