소수찾기 · Gilbert

문제 파악

문제

주요 조건

• 11과 011은 같은 숫자로 취급한다.

• 012은 숫자 0, 1, 3이 흩어저 있다는 의미

입출력 예시

numbers	return
“17”	3
“011”	2

문제 해결 과정

핵심 로직

소수 : 1과 자기 자신 외의 약수를 가지지 않는 1보다 큰 자연수

주어진 숫자로 만들수 있는 모든 숫자를 만든다. ➡️ 순열

조합된 숫자 중 소수를 구한다.

해결 순서

이번 문제의 해결 순서는 아래와 같다.

⒈ 주어진 문자열을 분리한다. [“17”] → [“1”,”2”]

⒉ 분리된 문자열을 조합해서 만들수 있는 모든 문자열을 만든다.

⒊ 조합된 숫자 중 소수를 구한다.

해결 순서는 간단하지만 모든 조합을 찾는다 라는 부분에서 막혔다. 이 문제를 해결하기 위해서는

순열 알고리즘에 대한 지식이 있어야 했다.

순열 알고리즘

순열이란?

순열이란 n개의 값 중에서 r개의 숫자를 모든 순서대로 뽑는 경우를 말한다.

순열 알고리즘 구현은 Swap을 이용하는 방법과 visited 배열을 사용하는 방법이 있다.

위 두 방법을 차례로 알아봤다.

✔︎ 순열과 조합의 차이

✔︎ 유사문제

⒈ Swap을 이용한 순열 알고리즘

Swap이란?

우선 swap의 정의에 대해서 알아보았다.

컴퓨터 프로그래밍에서 교체연산 또는 스왑 알고리즘은 두 변수에 들어 있는 값을 서로 맞바꾸는

연산 또는 이러한 연산을 사용하는 알고리즘이다. 예를 들어 만약 변수 a와 b가 각각 2와 3이라는

정수 값이 들어 있을 때, 스왑 명령을 실행하면 두 변수의 값은 각각 3과 2로 변한다.

교체 연산은 많은 알고리즘들에서 사용된다. 대표적으로 많은 정렬 알고리즘은 값들의 순서를

바꾸기 위해 교체 연산을 사용한다.

Swap의 구현

Swap(교체 연산)은 임시 변수 를 도입하여 구현할 수 있다.

int a = 1;
int b = 2;
int c;

c = a;
a = b;
b = c;

이 외에 방법들은 여기서 확인할 수 있다.

순열 구현

파라미터	설명
arr	기본 제공 배열
depth	재귀 깊이
n	nPr의 n
r	nPr의 r

public class SwapPurmuation {

    public static void main(String[] args) {

        int[] arr = {1, 2, 3};
        permutation(arr, 0, 3, 3);

    }

    // 순열
    public static void permutaion(int[] arr, int depth, int n, int r) {

        // 탈출 조건
        if (depth == r) {
            String joiningElements = Arrays.stream(arr)
                                        .mapToObj(String::valueOf)
                                        .collect(Collectors.joining());
            System.out.println(joiningElements)
        }

        for (int i = depth; i < n; i++) {    
            // arr[depth] ↔️ arr[i]
            swap(arr, depth, i);

            // depth + 1
            permutation(arr, depth + 1, n, r);

            // 탈출조건 만족시 배열 원상복귀
            swap(arr, depth, i);
        }

    // Swap
    public static void swap(arr, depth, i) {
        int temp = arr[depth];
        int arr[i] = arr[depth];
        int arr[depth] = temp;
    }

}

// 출력결과 : 123, 132, 213, 231, 321, 312

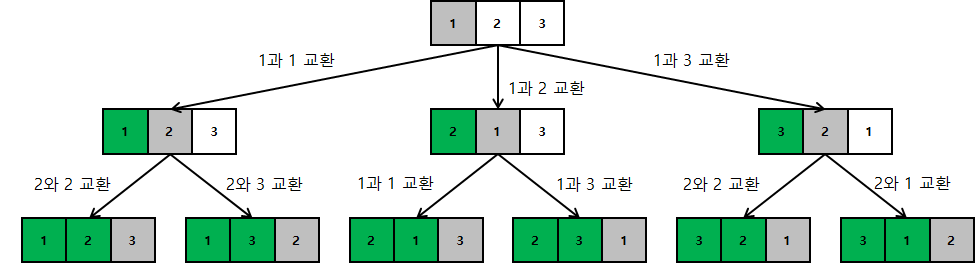
⒉ Visited 배열을 사용한 순열 구현

Visited 배열을 사용하는 방식은 Swap과는 다르게 순서를 지킨다.

파라미터	설명
arr	배열
output	DFS를 돌면서 노드를 넣어준다.
visited	노드 방문 여부 확인
n	nPr의 n
r	nPr의 r

public class permutation {

    public static void main(String[] args) {
        int[] arr = {1, 2, 3};
        boolean[] visited = new boolean[arr.length];
        int[] output = new int[arr.length];

        for (int i = 0; i < arr.length; i++) {
            permutation(arr, output, visited, 0, arr.length, i+1);
        }
    }

    // 순열
    public static void permutation(int[] arr, int[] output, boolean[] visited, int depth, int n, int r) {

        // 탈출 조건
        if (depth == r) {
            int[] temp = Arrys.copyOfRange(output, 0, depth);
            String result = Arrays.stream(temp).mapToObj(String::valueOf).collect(Collectors.joining());
            System.out.println(result);
        }

        for (int i = 0; i < n; i++) {
            if (!visited[i]) {
                visited[i] = true;
                output[depth] = arr[i];
                permutation(arr, output, visited, depth + 1, n , r);
                visited[i] = false;
            }
        }
    }
}

✅ Arrays.copyOfRange(원본 배열, 복사할 시작인덱스, 복사할 끝인덱스)

위 함수를 사용한 이유는 3개의 숫자중 하나 혹은 두 개의 숫자를 선택할 경우에,

3번 째 값을 넣을 필요가 없다. 코드에서 해당 코드를 빼고 실행하게 되면

결과
100, 232, 331, 121, 133, 212, 233, 311, 322, 123, 132, 213, 231, 312, 321

위의 표와 같이 결과가 나오는데 자세히 보면 중복되는 요소가 들어간다.

즉, 위 함수는 불필요한 요소는 무시하고 필요한 위치의 요소만 가져오기 위함이다.

소스 코드

🔖 소스 코드

import java.util.Arrays;
import java.util.HashSet;
import java.util.stream.Collectors;

public class quiz42839 {

    static HashSet<String> setList = new HashSet<>();

    public static void main(String[] args) {

        String numbers = "017";
        int[] arr = Arrays.stream(number.split("")).mapToInt(Integer::parseInt).toArray();
        int[] output = new int[arr.length];
        boolean[] visited = new boolean[arr.length];

        // 순열
        for (int i = 0; i < arr.length; i++) {
            permutation(arr, output, visited, 0, arr.length, i + 1);
        }

        // 소수 판별
        for (Integer element : setList) {
            if (isPrimeNum(element)) {
                answer ++;
            }
        }

        System.out.println(answer);
    }

    // 순열
    public static void permuataion(int[] arr, int[] ouptut, boolean[] visited, int depth, int n, int r) {

        // 탈출 조건
        if (depth == r) {
            int[] temp = Arrays.copyOfRange(output, 0, depth);
            String result = Arrays.stream(temp).mapToObj(String::valueOf).collect(Collectors.joining());
            setList.add(Integer.valueOf(result));
        }

        for (int i = 0; i < n; i++) {
            if (!visited[i]) {
                visited[i] = true;
                output[depth] = arr[i];
                permutation(arr, output, visited, depth + 1, n, r);
                visited[i] = false;
            }
        }
    }

    // 소수 찾기(에라토네스의 체)
    public static boolean isPrimeNum(int num) {
        if (num == 0 || num == 1) {
            return false;
        }

        for (int i = 2; i <= Math.sqrt(num); i++) {
            if (num % i == 0) {
                return false;
            } 
            return true;
        }
    }
}