연결 요소의 개수

문제 파악

문제

주요 조건

• 서로 연결된 노드가 없다는 것을 파악하기

TEST CASE

Test Case
6 5
1 2
2 5
5 1
3 4
4 6

문제 해결 과정

핵심 로직

• 서로 연결되지 않은 노드도 있기 때문에 n번의 DFS로직이 실행되어야 한다.

해결 순서

해당 문제는 DFS를 구현해서 풀이를 하였다.

단 이번 문제에서는 아래와 같이 노드들 끼리 연결이 되지 않는 경우도 있다.

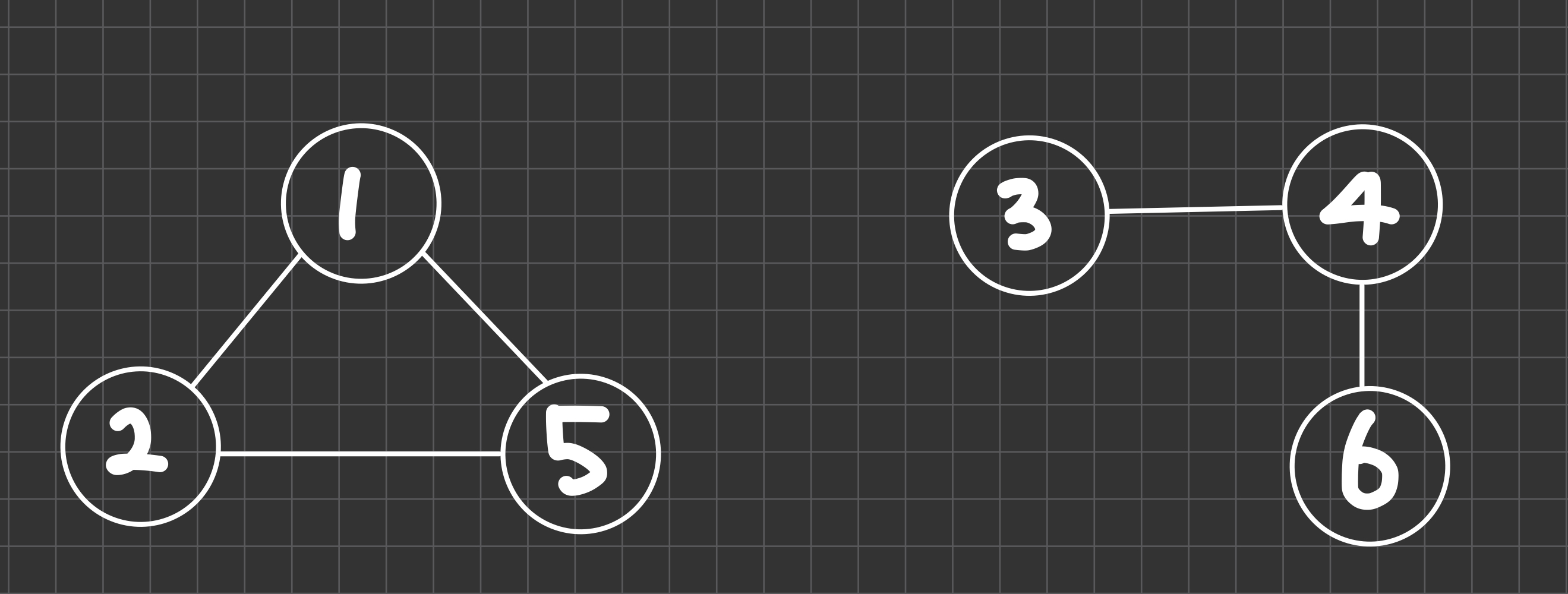
위와 같은 경우라면 DFS로직이 두 번 실행되어야 한다.

⒈ 인접 행렬을 생성한다.

⒉ N개의 노드를 순회한다.

⒊ 만약 i번째 노드를 방문하지 않았다면, DFS로직이 실행된다.

⒋ DFS로직이 끝나면 로직수행 횟수에 1을 더해준다.

소스 코드

🔖 소스 코드

import java.io.BufferedReader;
import java.io.IOException;
import java.io.InputStreamReader;
import java.util.StringTokenizer;

public class 연결요소의수 {

    static int n, m, a, b, answer;
    static int[][] graph;
    static boolean[] visited;

    public static void main(String[] args) throws IOException {
        BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
        StringTokenizer st = new StringTokenizer(br.readLine(), " ");
        n = Integer.parseInt(st.nextToken());
        m = Integer.parseInt(st.nextToken());

        graph = new int[n+1][n+1];
        visited = new boolean[n+1];

        for (int i = 0; i < m; i++) {
            st = new StringTokenizer(br.readLine(), " ");
            a = Integer.parseInt(st.nextToken());
            b = Integer.parseInt(st.nextToken());

            graph[a][b] = graph[b][a] = 1;
        }

        for (int j = 1; j <= n; j++) {
            if (!visited[j]) {
                dfs(j);
                answer ++;
            }
        }
        System.out.println(answer);
    }

    private static void dfs(int node) {

        visited[node] = true;

        int[] neighborNodes = graph[node];

        for (int i = 0; i < neighborNodes.length; i++) {
            if (!visited[i] && neighborNodes[i] == 1) {
                dfs(i);
            }
        }
    }
}